Arreglos serie - paralelo de resistencias
Resolver arreglos de resistencias conectadas en serie y paralelo es una tarea habitual en el análisis de circuitos. Con una metodología clara, es posible simplificar incluso combinaciones aparentemente complejas de forma ordenada y precisa.
Conexión en serie
Las resistencias están en serie cuando están conectadas una después de la otra, compartiendo un solo camino para la corriente.
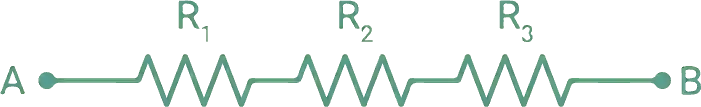
La resistencia equivalente en serie se obtiene simplemente sumando todas las resistencias:
Req = R₁ + R₂ + R₃ + ... + Rn
Conexión en paralelo
En una conexión en paralelo, las resistencias se conectan de tal forma que tienen los mismos puntos de inicio y fin. En este tipo de arreglos, la corriente se divide entre ellas y el voltaje es el mismo entre los puntos A y B.
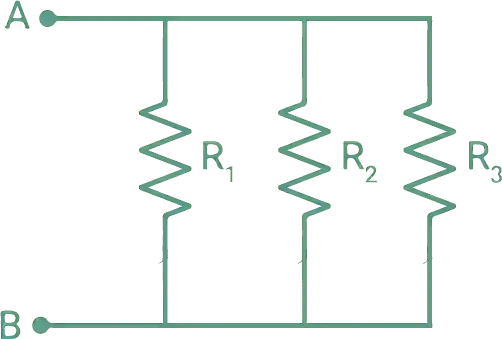
La resistencia equivalente es:
1 / Req =1 / R₁ + 1 / R₂ + 1 / R₃ + ... + 1 / Rn
¿Cómo resolver un arreglo combinado?
La clave está en identificar primero los bloques o ramales que estén puramente en serie o puramente en paralelo, resolverlos, y luego avanzar paso a paso hasta que el circuito quede completamente simplificado.
Pasos básicos:
✔️ Identifica las resistencias en serie y calcula su resistencia equivalente.
✔️ Identifica las resistencias en paralelo y calcula su resistencia equivalente.
✔️ Redibuja el circuito con los nuevos valores obtenidos.
✔️ Repite hasta que tengas una sola resistencia equivalente.
Un ejemplo sencillo
Supongamos el siguiente arreglo: R₁ = 4Ω en serie con un grupo paralelo formado por R₂ = 6Ω y R₃ = 3Ω.
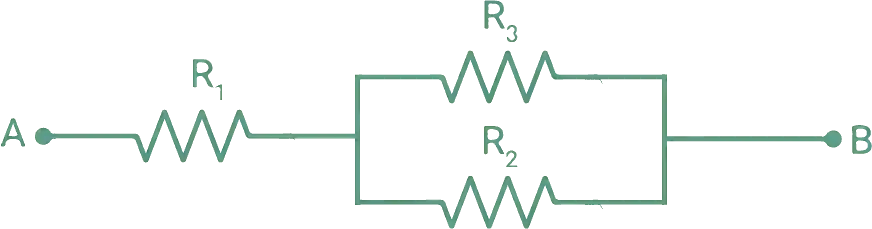
Primero, resolvemos el paralelo:
1 / Rp = 1/6 + 1/3 → Rp = 2Ω
Ahora sumamos R₁ en serie:
Req = 4Ω + 2Ω = 6Ω
¿Y qué pasa con las impedancias?
Los mismos principios que aplicamos para resistencias, también funcionan para impedancias en circuitos de corriente alterna.
La única diferencia es que las impedancias pueden tener valores complejos (parte real y parte imaginaria), pero la forma de combinarlas sigue siendo:
Zeq en serie: Z₁ + Z₂ + Z₃ + ... + Zn
1 / Zeq en paralelo: 1/Z₁ + 1/Z₂ + 1/Z₃ + ... + 1/Zn
Así que, si sabes simplificar resistencias, ¡ya tienes medio camino recorrido para resolver arreglos de impedancias!
En resumen
Resolver circuitos con arreglos serie-paralelo de resistencias o impedancias requiere aplicar dos conceptos fundamentales: la suma directa de resistencias, cuando el arreglo es en serie y la combinación recíproca de resistencias, cuando es en paralelo.